
Math Museum / NYC

Light Grooves, 2012 / Matthew Brand / Z-intaglio in alloy

 |
Harmony of the Spheres / Dmitri Tymoczko
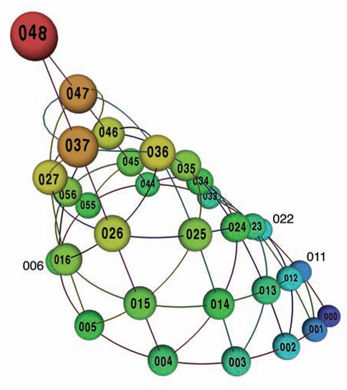
The space of three-note chord types is a cone. Numbers refer to pitch classes, with 0 = C, 1 = C#, etc. Points represent equivalence classes of transpositionally related chords. Thus, (C, D, E) and (D, E, F#) are both instances of 024. (Image made with Dmitri Tymoczko's "ChordGeometries" program available here.)  Geometrical music theory represents a culminating moment in the longstanding marriage of music and math. That marriage began when Pythagoras described pleasing musical intervals with simple mathematical ratios more than 2,600 years ago and further evolved during the Middle Ages when deep thinkers used those same ratios to model the "music of the spheres"—what many at that time believed to be the literally harmonious movements of the sun, moon and planets. Geometrical music theory represents a culminating moment in the longstanding marriage of music and math. That marriage began when Pythagoras described pleasing musical intervals with simple mathematical ratios more than 2,600 years ago and further evolved during the Middle Ages when deep thinkers used those same ratios to model the "music of the spheres"—what many at that time believed to be the literally harmonious movements of the sun, moon and planets.
 ( via ) ( via )
 Western musicians traditionally classify pitch sequences by disregarding the effects of five musical transformations: octave shift, permutation, transposition, inversion, and cardinality change. We model this process mathematically, showing that it produces 32 equivalence relations on chords, 243 equivalence relations on chord sequences, and 32 families of geometrical quotient spaces, in which both chords and chord sequences are represented. This model reveals connections between music-theoretical concepts, yields new analytical tools, unifies existing geometrical representations, and suggests a way to understand similarity between chord types. Western musicians traditionally classify pitch sequences by disregarding the effects of five musical transformations: octave shift, permutation, transposition, inversion, and cardinality change. We model this process mathematically, showing that it produces 32 equivalence relations on chords, 243 equivalence relations on chord sequences, and 32 families of geometrical quotient spaces, in which both chords and chord sequences are represented. This model reveals connections between music-theoretical concepts, yields new analytical tools, unifies existing geometrical representations, and suggests a way to understand similarity between chord types.
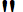 ( via ) ( via )
|

Branching Sway


<< NEWER OLDER >>